When you’re working in data science and analytics, handling high-dimensional data is a part of it. You may have a dataset with 600 or even 6000 variables, with some columns that prove to be important in modelling, while some that are insignificant, some correlated to each other (i.e. weight and height) and some entirely independent of one another.
Because handling thousands of features is both difficult and inefficient, our aim is to reduce the dataset to fewer independent features that capture most of the original information.
When we reduce data from many dimensions to fewer dimensions, we use a statistical approach combined with data compression. This method is known as Principal Component Analysis (PCA).
What is Dimensionality Reduction?
Dimension reduction means simplifying a dataset by reducing the number of dimensions and focusing on the key features. It can also be described as a method that simplifies a high-dimensional dataset into fewer dimensions by focusing on the key features.
Dimensionality reduction is helpful when dealing with datasets that contain a large number of variables. Some of the widely used dimensionality reduction techniques include Principal Component Analysis, Wavelet Transforms, Singular Value Decomposition, Linear Discriminant Analysis, and Generalized Discriminant Analysis.
What is Principal Component Analysis?
Principal Component Analysis is a key method that helps simplify data by reducing its dimensions during preprocessing. It is an unsupervised technique used for reducing the number of dimensions in a dataset.
It considers the variance within the data points and does not use any information about class labels. We reduce the data by looking at how much the data points vary, without using the class labels or dependent variables.
Steps in Principal Component Analysis with R
These are the few steps in principal component analysis
1. Making the input data consistent by standardizing it.
2. Computation of the covariance matrix for standardized dataset values.
3. Finding the eigenvalues and eigenvectors of the covariance matrix.
4. Sorting the eigenvalues and eigen vectors .
5. Extract the principal components from the data and construct a new feature.
6. Map the data onto the principal component axes.
In this article, we aim to achieve three main objectives:
1. Understanding the need for dimension reduction
2. Performing PCA and analyzing data variation & data composition
3. Determining features that prove to be most useful in data discernment
PCA produces principal components (equal to the number of features) that are ranked in order of variance (PC1 shows the most variance, PC2 the second most, and so on…).
To understand this in more detail, we will work on a sample dataset using the prcomp() function in R. I used a dataset from data.world, an open platform, which shows the nutrient content of different pizza brands. To simplify our analysis, the .csv file contains only the A, B, and C pizza brands.
Step 1: Importing libraries and reading the dataset into a table
Make sure your .csv file is in the current folder. You can check the folder with getwd() or change it with setwd().
library(dplyr)
library(data.table)
library(datasets)
library(ggplot2)
data <- data.table(read.csv(“Pizza.csv”))
Step 2: Making sense of the data
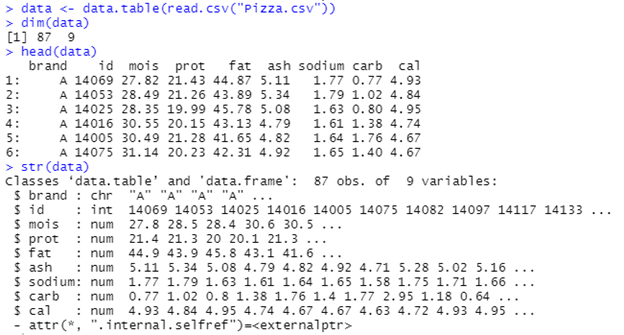
These functions tell you a) the dimensions i.e. rows x columns of the matrix b) the first few rows of the data and c) the datatypes of the variables.
dim(data)
head(data)
str(data)
Basic Initial Function
Step 3: Getting the principal components
We want to make our target variable NULL since we want our analysis to tell us the different types of pizza brands there are. Once we have done that and copied our dataset to keep the original values, we’ll runt prcomp() with .scale = TRUE so that the variables are scaled to unit variance before the analysis.
pizzas <- copy(data) pizzas <- pizza[, brand := NULL] pca <- prcomp(pizzas, scale. = TRUE)
The important thing to know about prcomp() is that it returns 3 things:
1. x: stores all the principal components of data that we can use to plot graphs and understand the correlations between the PCs.
2. sdev: calculates the standard deviation to know how much variation each PC has in the data
3. rotation: determines which loading scores have the largest effect on the PCA plot i.e., the largest coordinates (in absolute terms)
Download PDF: Principal Component Analysis with R: How to Reduce Dimensionality
Step 4: Using x
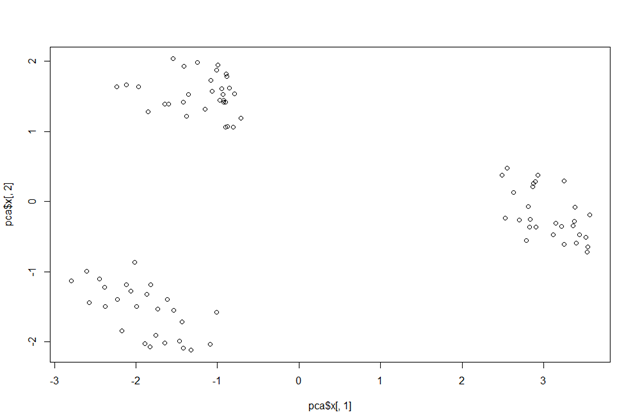
Even though currently our data has more than two dimensions, we can plot our graph using x. Usually, the first few PCs capture maximum variance, hence PC1 and PC2 are plotted below to understand the data.
pca_1_2 <- data.frame(pca$x[, 1:2]) plot(pca$x[,1], pca$x[,2])
PC1 against PC2 plot
This plot clearly shows us how the first two PCSs divide the data into three clusters (or A, B & C pizza brands) depending on the characteristics that define them.
Step 5: Using sdev
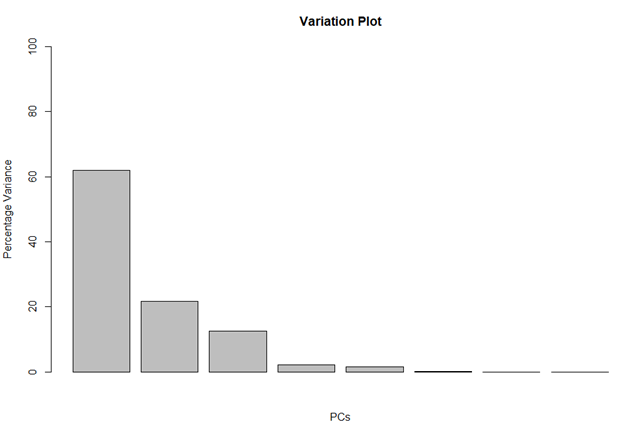
Here, we use the square of sdev and calculate the percentage of variation each PC has.
pca_var <- pca$sdev^2 pca_var_perc <- round(pca_var/sum(pca_var) * 100, 1) barplot(pca_var_perc, main = "Variation Plot", xlab = "PCs", ylab = "Percentage Variance", ylim = c(0, 100))
Percentage Variation Plot
This barplot tells us that almost 60% of the variation in the data is shown by PC1, 20% by PC2, 12% by PC3 and then very little is captured by the rest of the PCs.
Step 6: Using rotation
This part explains which of the features matter the most in separating the pizza brands from each other; rotation assigns weights to the features (technically called loadings) and an array of ‘loadings’ for a PC is called an eigenvector.
PC1 <- pca$rotation[,1] PC1_scores <- abs(PC1) PC1_scores_ordered <- sort(PC1_scores, decreasing = TRUE) names(PC1_scores_ordered)

We see how the variable ‘cal’ (Amount of calories per 100 grams in the sample) is the most important feature in differentiating between the brands, while ‘mois’ (Amount of water per 100 grams in the sample) is next and so on.
Step 7: Differentiating between brands using the two most important features
ggplot(data, aes(x=data$cal, y=data$mois, color = data$brand)) + geom_point() + labs(title = "Pizza brands by two variables")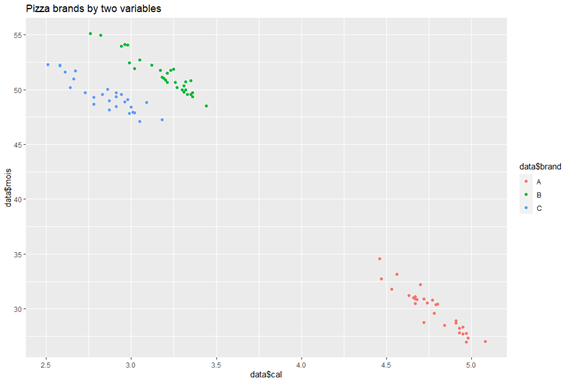
Cluster Formation via Most Weighted Columns
This plot clearly shows how, instead of the 8 columns given to us in the dataset, only two were enough to understand we had three different types of pizzas, thus making PCA a successful analytical tool to reduce high-dimensional data into a lower one for modelling and analytical purposes.